정렬되지 않은 배열을 스왑 기반 정렬(버블, 선택, 삽입 등)로 정렬할 때, 총 스왑 횟수를 구하라.
이 문제는 Inversion Counting 또는 Inversion Index로 불리는 유명한 문제다. (인터넷에서는 Inversion Counting이라는 용어가 더 알려져 있으므로 게시글에서는 Inversion Counting이라 부른다.)
이 게시글에서는 Inversion Counting을 펜윅 트리(Binary Indexed Tree)로 푸는 방법을 소개한다.
어떻게 푸는가?
우리는 배열 A의 i번째 원소 A[i] 뒤에 A[i]보다 작은 원소가 몇 개 존재하는지 펜윅 트리로 저장할 것이다.
그 값을 val이라고 했을 때 i번째 인덱스 뒤에 A[i]보다 작은 원소가 없게 하기 위해 val번 만큼 swap을 해야 하는 것으로 이해할 수 있다.

이 배열의 inversion counting을 해보자.

배열의 끝부터 순회를 시작한다. 배열의 끝이므로 2보다 작은 원소는 없다.

3보다 작은 원소는 {2} 한 개가 있다. 3은 제자리를 찾아가기 위해 2와 스왑해야 하므로 스왑 횟수는 1이 추가된다.

4보다 작은 원소는 {3, 2}가 있다. 4가 제자리를 찾아가기 위해 두 번의 스왑을 해야 하므로 스왑 횟수는 2가 추가된다.
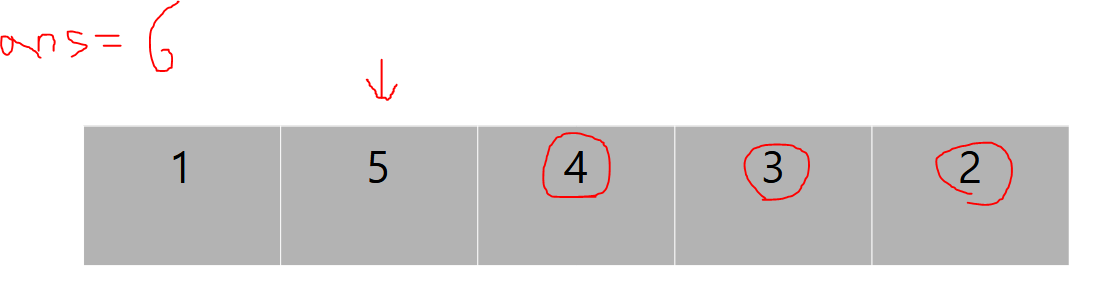
5보다 작은 원소는 3개가 있으므로 세 번의 스왑을 해야 한다. 따라서 스왑 횟수는 3이 추가된다.
마지막 1은 제자리를 지키고 있으므로 횟수의 변화가 없다. 따라서 이 배열의 Inversion Counting은 6이다.
펜윅 트리에 적용
이론은 알겠으나 이를 어떻게 펜윅 트리에 적용하는지 감이 오지 않을 수 있다. 코드를 통해 이해해보도록 하자.
// inversion counting을 저장하는 변수
ll res = 0;
// 배열의 뒤부터 검사하므로 그 크기인 n부터 1까지 for loop
for (int j = n; j >= 1; --j)
{
// 호출되는 함수 인자 중 fenwick은 펜윅 트리를 나타내는 벡터이다
// 원소의 좌표 압축 결과 index 가져오기
int num = idx[j];
// num - 1까지의 출현 횟수 더하기
res += sum(fenwick, num - 1);
// 현재 원소가 출현했음을 BIT에 반영
add(fenwick, num, 1);
}sum(fenwick, num - 1)로 자기보다 작은 원소에 저장된 값을 inversion counting에 더한 다음 add(fenwick, num, 1)을 호출하여 현재 원소가 존재하는 구간에 1을 더하는 것을 볼 수 있다.
loop는 n부터 시작하므로 "A[i] 뒤에 A[i]보다 작은 원소가 몇 개 존재하는지" 이 조건을 충족하면서 inversion counting을 할 수 있다.
그리고 add 함수를 통해 해당 원소가 나타남을 펜윅 트리에 반영하게 된다. 이를 통해 다음 index에서 자기보다 작은 원소의 갯수를 sum 함수로 간단히 구할 수 있게 된다.
해보자
1. 펜윅 트리 준비
펜윅 트리를 준비한다.
2. 배열 원소의 좌표 압축
배열의 크기와 원소가 가질 수 있는 수의 범위가 서로 다른 경우 펜윅 트리를 그대로 사용할 수 없다.
좌표 압축을 통해 원소 값의 상한이 배열 크기 이내로 들어오도록 조정한다.
좌표 압축을 모르는 경우는 여기를 참조한다.
3. Inversion Couning 수행
위에 설명한 코드를 통해 inversion counting을 하면 쉽게 답을 구할 수 있다.
유의점
계산 도중 index의 out of bound를 방지하기 위해 시작 index는 1로 하는 것을 권고한다.
마지막으로 Inversion Counting을 구하는 문제인 1517 - 버블 소트의 정답 코드를 첨부하며 게시글을 마친다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int ar[500001];
int idx[500001];
vector<int> crd;
inline int get_idx(int val)
{
return (lower_bound(crd.begin(), crd.end(), val) - crd.begin()) + 1;
}
ll sum(vector<ll> &tree, int pos)
{
ll res = 0;
while (pos)
{
res += tree[pos];
pos &= (pos - 1);
}
return res;
}
void add(vector<ll> &tree, int pos, ll val)
{
while (pos < tree.size())
{
tree[pos] += val;
pos += (pos & -pos);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> ar[i];
crd.push_back(ar[i]);
}
vector<ll> fenwick(n + 1);
sort(crd.begin(), crd.end());
crd.erase(unique(crd.begin(), crd.end()), crd.end());
for (int i = 1; i <= n; ++i)
idx[i] = get_idx(ar[i]);
ll res = 0;
for (int j = n; j >= 1; --j)
{
int num = idx[j];
res += sum(fenwick, num - 1);
add(fenwick, num, 1);
}
cout << res;
}
'CP Algorithm & Knowledge' 카테고리의 다른 글
| 세그먼트 트리로 k번째 작은 수 찾기 (0) | 2021.07.08 |
|---|---|
| 좌표 압축 - 원소의 밀도를 높이자 (0) | 2021.07.03 |
| 단조 큐 (Monotone Queue) (0) | 2021.01.26 |
| 지그재그 순열(Alternating Permutaion) 의 개수 구하기 (1) | 2021.01.02 |
| MST 최소 신장 트리 Sollin, Boruvka (솔린, 보르부카) 알고리즘 구현 (0) | 2020.12.20 |