728x90
https://www.acmicpc.net/problem/2104
문제에서 요구하는 사항을 처리하기 위해서는 두 개의 세그먼트 트리가 필요하다.
하나는 구간합을 저장하는 트리, 나머지는 구간의 최솟값의 index를 저장하는 트리이다.
최솟값도 아니고 그 index를 저장하는 이유는 다음 전략을 따르기 때문이다.
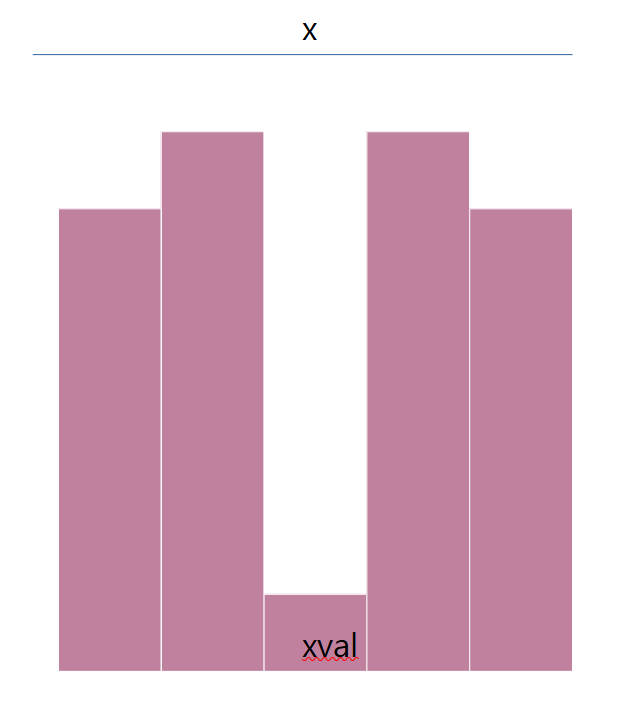
1. 특정 구간 x의 연산 결과를 구한다.
2. x의 최소 원소 xval가 없는 구간은 xval보다 큰 수를 곱할 것이 자명하다.
3. 그렇다면 xval이 빠진 구간의 연산 결과는 구간 x의 연산 결과보다 커질 수 있다는 기대를 가질 수 있다.(입력은 전부 1 이상의 정수이므로 더하는 것보다 곱하는게 더 영향이 크다는 사실을 상기하라.)
4. 그러므로 우리는 xval를 pivot으로 하여 구간을 두 개씩 분할해 최댓값을 찾을 수 있다.
이 전략을 구현하기 위해 구간합을 구하는 세그먼트 트리, 구간 최솟값의 index를 구하는 세그먼트 트리를 만들어서 연산의 최댓값을 찾아나가면 된다.
자세한 구현은 밑에 있는 코드에서 참조할 수 있다.
전체 코드
더보기
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int ar[100001];
int n;
vector<int> seg_idx;
inline int mid(int s, int e) { return s + (e - s) / 2; }
int cmpidx(int a, int b)
{
if (a == -1) return b;
if (b == -1) return a;
if (ar[a] < ar[b]) return a;
return b;
}
int init_min(int node, int start, int end)
{
if (start == end) return seg_idx[node] = end;
int m = mid(start, end);
int l = init_min(node * 2, start, m);
int r = init_min(node * 2 + 1, m + 1, end);
return seg_idx[node] = cmpidx(l, r);
}
int query_min(int node, int start, int end, int l, int r)
{
if (start > r || end < l) return -1;
if (l <= start && end <= r) return seg_idx[node];
int m = mid(start, end);
return cmpidx(
query_min(node * 2, start, m, l, r),
query_min(node * 2 + 1, m + 1, end, l, r)
);
}
ll init_sum(vector<ll> &tree, int node, int start, int end)
{
if (start == end) return tree[node] = ar[end];
int m = mid(start, end);
return tree[node] = init_sum(tree, node * 2, start, m) + init_sum(tree, node * 2 + 1, m + 1, end);
}
ll query_sum(vector<ll> &tree, int node, int start, int end, int l, int r)
{
if (start > r || l > end) return 0;
if (l <= start && end <= r) return tree[node];
int m = mid(start, end);
return query_sum(tree, node * 2, start, m, l, r) + query_sum(tree, node * 2 + 1, m + 1, end, l, r);
}
ll query(vector<ll> &tree, int start, int end)
{
if (start == end) return (ll)ar[end] * ar[end];
int idx = query_min(1, 1, n, start, end);
ll res = ar[idx] * query_sum(tree, 1, 1, n, start, end);
if (start < idx) res = max(res, query(tree, start, idx - 1));
if (idx < end) res = max(res, query(tree, idx + 1, end));
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
seg_idx.resize(n * 4);
vector<ll> sum_tree(n * 4);
for (int i = 1; i <= n; ++i)
cin >> ar[i];
init_min(1, 1, n);
init_sum(sum_tree, 1, 1, n);
cout << query(sum_tree, 1, n);
}
728x90
'백준 > 세그먼트 트리' 카테고리의 다른 글
| [ICPC] 백준 5012 - 불만 정렬 (0) | 2021.07.21 |
|---|---|
| [COCI] 백준 3006 - 터보 소트 (0) | 2021.07.20 |
| [ICPC] 백준 9345 - 디지털 비디오 디스크 (0) | 2021.07.14 |
| 백준 13544 - 수열과 쿼리 3 (0) | 2021.07.13 |
| [ICPC] 백준 7469 - K번째 수 (0) | 2021.07.10 |



