https://www.acmicpc.net/problem/2169
힌트 1
주어진 상태 공간에서 방향을 반영한 DP 테이블을 설계할 수 있다. DP 테이블을 만들 수 있겠는가?
힌트 2
이 문제를 바텀 업 DP로 해결을 시도할 경우 $2MN$번 반복문을 돌아야 할 것이다.
혹시 자기의 코드가 $NM$번 반복문을 돌고 있을 경우 무엇을 빠트렸는지 생각해보자.
힌트 3
최장 경로를 찾아야 하면서도 입력 값에 음수가 들어간다. 혹시 DP 테이블 초기화에 문제가 있진 않는지 점검한다.
풀이
3방향으로 로봇이 움직이면서 최장 경로를 찾는 문제이다.
$N, M \leq 1000$ 임을 감안하여 우리는 다음과 같은 DP 테이블을 생각할 수 있다.
dp[i][j][k] := k방향으로 좌표 (i, j)에 도착했을 때 최댓값
k는 단지 3방향을 표현하므로 메모리에 큰 부담이 되지 않는다.
그러면 아래 방향을 0, 오른쪽 방향을 1, 왼쪽 방향을 2로 놓고 특정 방향으로 갔을 때의 최댓값을 계산할 수 있다.
이때 한번 방문한 지점은 다시 가면 안된다는 제약이 있으므로 오른쪽과 왼쪽 방향에 대해서는 조건 검사를 해서 왼쪽으로부터 온 로봇을 다시 왼쪽으로 보내는 일이 있어선 안된다.(오른쪽도 마찬가지)
이렇게 최대 3방향으로 분기를 계산해서 목적지에 도착했을 때 최대값을 출력하면 된다.
다만 구현에서는 유의할 점이 있다.
이중 반복문(i, j)으로 통한 바텀 업 DP를 계산할 때 j에 대해 두 번 반복문을 돌려야 한다.
왼쪽에서 오른쪽으로 가는 경우, 오른쪽에서 왼쪽으로 가는 경우를 둘 다 계산해주기 위함이다.
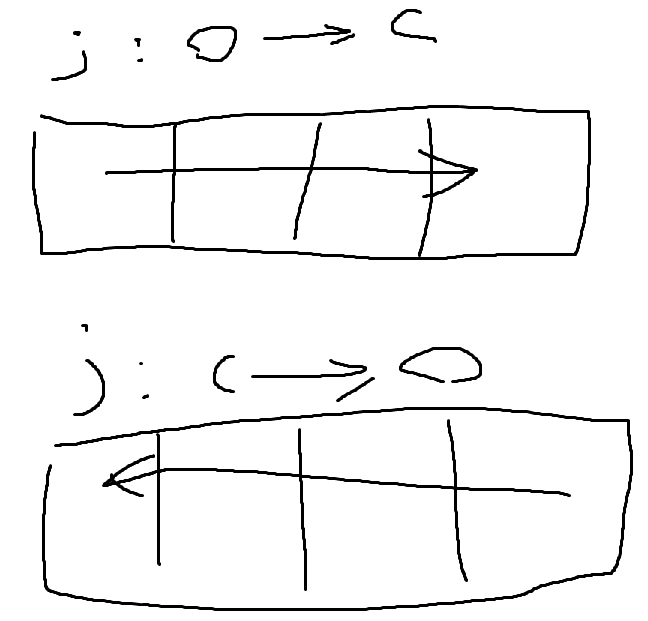
만약 한쪽이 빠질 경우 그 빠진 한쪽 방향으로 갔을 때의 최적해를 계산할 수 없게 된다.
또한 주어진 입력값들이 음수만 있는 경우를 대비하기 위해 DP 테이블을 아주 적절히 큰 음수로 초기화하는 것을 잊지 말도록 하자.
위 사항을 주의하며 DP를 수행하면 정답을 받을 수 있다.
전체 코드
// #pragma GCC target("avx,avx2,fma")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("unroll-loops")
#include <bits/stdc++.h>
using namespace std;
int dp[1000][1000][3];
int ar[1000][1000];
int r, c;
int main()
{
cin.tie(nullptr);
ios::sync_with_stdio(false);
cin >> r >> c;
for (int i = 0; i < r; ++i)
for (int j = 0; j < c; ++j)
cin >> ar[i][j];
fill(&dp[0][0][0], &dp[0][0][0] + 1000 * 1000 * 3, -1e9);
dp[0][0][0] = dp[0][0][1] = ar[0][0];
for (int i = 0; i < r; ++i)
{
for (int j = 0; j < c; ++j)
{
if (i + 1 < r)
{
for (int k = 0; k < 3; ++k)
{
dp[i + 1][j][0] = max(dp[i + 1][j][0], dp[i][j][k] + ar[i + 1][j]);
}
}
if (j)
{
dp[i][j - 1][2] = max(dp[i][j - 1][2], dp[i][j][2] + ar[i][j - 1]);
dp[i][j - 1][2] = max(dp[i][j - 1][2], dp[i][j][0] + ar[i][j - 1]);
}
if (j + 1 < c)
{
dp[i][j + 1][1] = max(dp[i][j + 1][1], dp[i][j][1] + ar[i][j + 1]);
dp[i][j + 1][1] = max(dp[i][j + 1][1], dp[i][j][0] + ar[i][j + 1]);
}
}
for (int j = c - 1; j >= 0; --j)
{
if (i + 1 < r)
{
for (int k = 0; k < 3; ++k)
{
dp[i + 1][j][0] = max(dp[i + 1][j][0], dp[i][j][k] + ar[i + 1][j]);
}
}
if (j)
{
dp[i][j - 1][2] = max(dp[i][j - 1][2], dp[i][j][2] + ar[i][j - 1]);
dp[i][j - 1][2] = max(dp[i][j - 1][2], dp[i][j][0] + ar[i][j - 1]);
}
if (j + 1 < c)
{
dp[i][j + 1][1] = max(dp[i][j + 1][1], dp[i][j][1] + ar[i][j + 1]);
dp[i][j + 1][1] = max(dp[i][j + 1][1], dp[i][j][0] + ar[i][j + 1]);
}
}
}
cout << max(max(dp[r - 1][c - 1][0], dp[r - 1][c - 1][1]), dp[r - 1][c - 1][2]);
}제출 기록

추천 문제
https://atcoder.jp/contests/abc210/tasks/abc210_d
게시글에 작성된 풀이의 구현과 비슷하게 위 링크로 첨부한 문제를 풀 수 있다. 도전해보자!
'백준 > DP' 카테고리의 다른 글
| [ICPC] 백준 11066 - 파일 합치기 (0) | 2021.11.06 |
|---|---|
| [KOI] 백준 2616 - 소형기관차 (0) | 2021.11.05 |
| 백준 13555 - 증가하는 부분 수열 (0) | 2021.07.22 |
| 백준 17409 - 증가 수열의 개수 (0) | 2021.07.22 |
| 백준 18249 - 욱제가 풀어야 하는 문제 (0) | 2021.07.19 |



