오일러 투어?
오일러 투어는 트리에서 백트래킹을 할 때 그 흔적을 남기는 순회로 볼 수 있다.
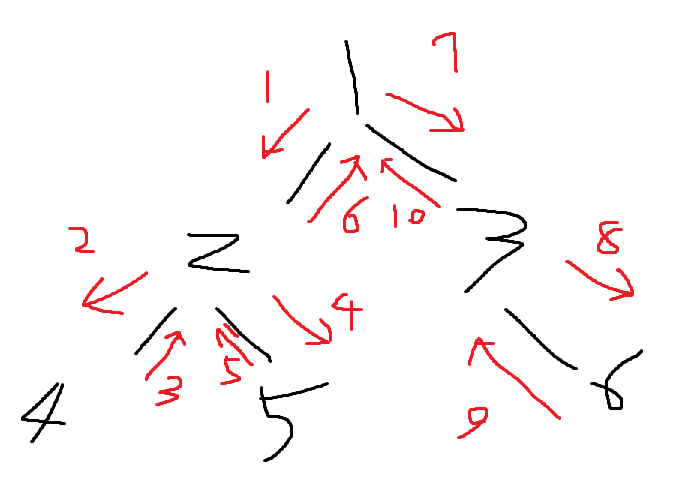
오일러 트리를 이용하면 DFS를 하면서 몇 번째 이동에 어떤 정점에 머무르는지, 어떤 부모 노드의 자식 중 가장 큰 번호가 무엇인지, 그리고 해당 정점이 어느 시점에 처음으로 방문되고 어느 시점에 마지막으로 방문되는지 파악할 수 있다.
오일러 투어로 무엇을 하려는지에 따라 그 구현이 달라지므로 위 경우들에 대한 구현을 소개한다.
1. x번째 이동에 도착한 정점
다음 코드는 DFS를 할 때 특정 시점에 방문한 노드를 기록한다.
vector<int> footprint;
vector<int> tree[100001];
bool discovered[100001];
void euler_tour(int node)
{
footprint.push_back(node);
for (int i: tree[node])
{
if (discovered[i])
continue;
discovered[i] = true;
euler_tour(i);
footprint.push_back(node);
}
}
우선 foot_print 벡터에 node를 삽입하여 현재 node번에 도착했음을 알린다.
그다음 트리의 자식을 대상으로 DFS를 하는데 만약 자식이 방문 가능하다면 그 자식의 탐색이 끝날 때 다시 한번 node를 삽입한다.
이는 자식을 대상으로 한 순회를 마치고 자기에게 돌아왔다는 뜻을 가진다.
순회가 모두 끝나면 몇 번째 이동에 도착한 노드가 무엇인지 foot_print 벡터에서 바로 확인할 수 있다.
2. 특정 노드의 처음 방문 시점과 마지막 방문 시점
1번과 비슷하지만 특정 노드에 방문한 첫 번째 시점과 마지막 시점을 바로 알고 싶은 경우 다음과 같이 구현하면 된다.
int num = 1;
vector<int> tree[100001];
pii tour_inout[100001];
bool discovered[100001];
void euler_tour(int node)
{
tour_inout[node].first = num++;
for (int i: tree[node])
{
if (discovered[i])
continue;
discovered[i] = true;
euler_tour(i);
}
tour_inout[node].second = num;
}
이러면 특정 노드의 자식에 대해 몇번 이동했는지 계산하기 편하다.
3. 특정 노드의 자손 중 가장 큰 번호 알아내기
DFS를 하면서 노드 번호를 새로 바꿔간다고 해보자. 그리고 특정 노드의 자손 수가 어느 정도인지, 그리고 마지막으로 방문한 자손이 몇 번인지 알고 싶으면 2번의 구현을 바꿔서 다음처럼 바꿀 수 있다.
int num;
vector<int> tree[100001];
pii tour_leaf[100001];
int node_conv[100001];
bool discovered[100001];
void euler_tour(int node)
{
node_conv[node] = tour_leaf[node].first = ++num;
for (int i: tree[node])
{
if (discovered[i])
continue;
discovered[i] = true;
euler_tour(i);
}
tour_leaf[node].second = num;
}
num이 2번 구현과 어떤 차이점이 있는지 주목하라. 2번에서는 num을 1로 초기화해서 후위식으로 1을 더한 후 탐색을 이어갔지만 이 구현에서는 num을 0으로 초기화한 후 전위식으로 num에 1을 더해가며 탐색을 하고 있다.
이렇게 되면 tour_leaf의 first에는 현재 노드의 새로운 번호, second에는 자기에게 방문한 마지막 시점이 아니라 자신의 자손 중 마지막으로 방문한 노드의 번호가 기록된다.
또한 node_conv 배열에 새롭게 바뀐 노드 번호가 기록된다.
이 방법을 사용하여 자손의 수와 마지막으로 방문한 자손의 번호를 알 수 있게 된다.
연습하기
오일러 투어를 사용하는 문제를 풀어보자.
https://atcoder.jp/contests/abc213/tasks/abc213_d
D - Takahashi Tour
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
오일러 투어를 알고있는 상태에서 읽어보면 매우 쉬우니 설명은 생략한다.
지금까지 오일러 투어에 대해 알아보고 구현법 3가지를 알아보았다.
다음엔 오일러 투어와 다른 알고리즘을 결합해서 풀 수 있는 문제를 알아보도록 하자.
'CP Algorithm & Knowledge' 카테고리의 다른 글
| imos법 imos method いもす法 (0) | 2021.09.05 |
|---|---|
| 오일러 투어(Euler Tour) 응용 feat. 2820 자동차 공장 (0) | 2021.08.29 |
| 오일러의 체(Linear Sieve)로 O(logn) 소인수 분해 하기 (0) | 2021.08.22 |
| 그래프에서 DFS로 사이클 찾기 (0) | 2021.08.11 |
| 타일 채우기 문제를 푸는 테크닉 1 (0) | 2021.08.05 |
