https://www.acmicpc.net/problem/4196
힌트
도미노를 그래프로 모델링하면 위상 정렬을 통해 진입 차수가 0인 노드의 개수를 세는 방법으로 접근할 수 있다. 하지만 이것으로는 부족하다.
도미노의 상태에 따라 사이클이 생성될 수도 있고 그렇지 않을 수도 있다.
다음 그래프를 보자.
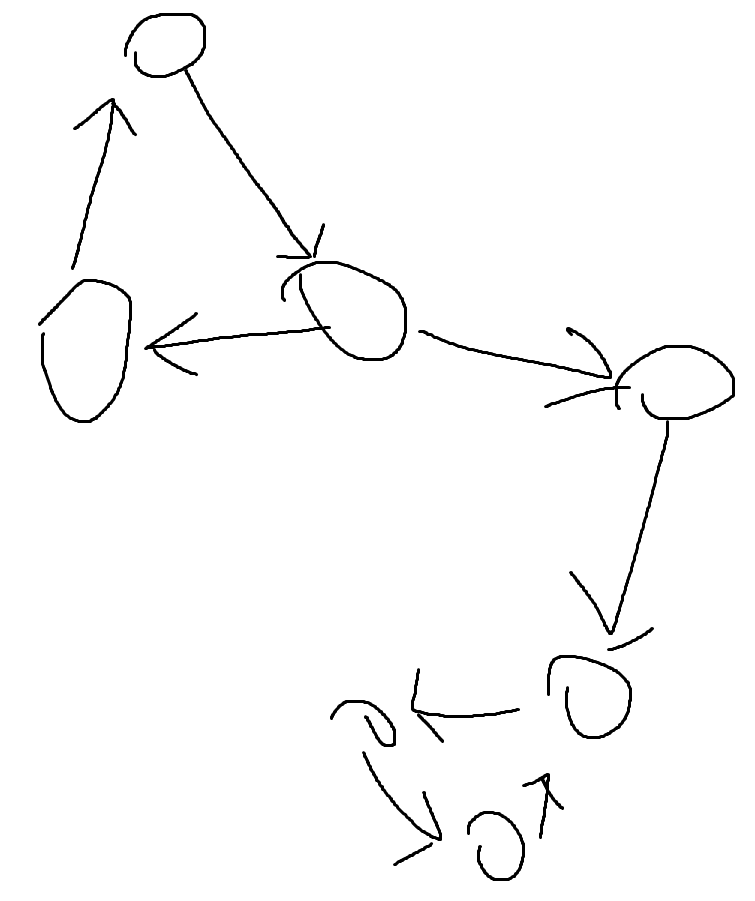
여기서 좌상단에 있는 사이클의 아무 도미노나 넘어트리면 모든 도미노를 넘어뜨릴 수 있다. 사이클을 영리하게 이용하는 방법을 생각해본다.
풀이
최소한의 시행으로 모든 도미노를 넘어뜨리기 위해서는 indegree가 0인 도미노만 건드려야 한다.
하지만 위에 힌트에서도 언급했듯이 어떤 도미노 집합이 사이클을 이루고 있는 경우에는 indegree가 0인 도미노가 없지만 해당 사이클에서 아무 도미노나 넘어뜨려도 모든 도미노를 넘어뜨릴 수 있다.
즉 우리는 도미노 각각의 indegree만 계산할 것이 아니라 사이클의 indegree도 계산해야 한다.
이를 효율적으로 계산하기 위해서는 SCC를 구해서 각 SCC의 indegree를 계산하도록 하면 된다.
구현하는 방법은 SCC를 구한 뒤 각 노드마다 해당하는 SCC 번호를 붙여준다.
그다음 한 번 더 DFS를 수행해서 현재 노드와 자식 노드의 SCC 번호가 같지 않을 때 자식에 속한 SCC의 indegree를 1 더해주면서 각 SCC의 indegree를 구할 수 있게 된다.
이렇게 indegree를 모두 구한 후 indegree가 0인 SCC의 갯수를 출력하면 된다.
전체 코드
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("unroll-loops")
#include <bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
#define NODE_MAX 100001
int node_scc[NODE_MAX];
int scc_indg[NODE_MAX];
int discovered[NODE_MAX];
bool finished[NODE_MAX];
vector<int> al[NODE_MAX];
stack<int> s;
int cnt;
vector<vector<int>> scc;
int dfs(int cur) {
int parent = discovered[cur] = cnt++;
s.push(cur);
for (int i: al[cur]) {
if (discovered[i] == -1) parent = min(parent, dfs(i));
else if (!finished[i]) parent = min(parent, discovered[i]);
}
if (parent == discovered[cur]) {
vector<int> group;
while (true) {
int t = s.top();
s.pop();
group.push_back(t);
finished[t] = true;
if (t == cur) break;
}
scc.push_back(group);
for (int i: group) node_scc[i] = scc.size();
}
return parent;
}
int t;
int v, e;
bool visited[NODE_MAX];
void scc_tour(int cur)
{
visited[cur] = true;
for (int i: al[cur])
{
if (node_scc[i] != node_scc[cur]) ++scc_indg[node_scc[i]];
if (visited[i]) continue;
scc_tour(i);
}
}
void solve()
{
cin >> t;
while (t--)
{
int ans = 0;
cin >> v >> e;
for (int i = 1; i < NODE_MAX; ++i) al[i].clear();
cnt = 0;
memset(discovered, -1, sizeof discovered);
memset(finished, 0, sizeof finished);
scc.clear();
memset(node_scc, 0, sizeof node_scc);
memset(scc_indg, 0, sizeof scc_indg);
memset(visited, 0, sizeof visited);
for (int i = 0; i < e; ++i)
{
int a, b;
cin >> a >> b;
al[a].push_back(b);
}
for (int i = 1; i <= v; ++i)
if (discovered[i] == -1) dfs(i);
for (int i = 1; i <= v; ++i)
if (!visited[i]) scc_tour(i);
for (int i = 1; i <= scc.size(); ++i)
if (scc_indg[i] == 0) ++ans;
cout << ans << '\n';
}
}
int main()
{
cin.tie(nullptr);
ios::sync_with_stdio(false);
solve();
}제출 기록

'백준 > 그래프' 카테고리의 다른 글
| [COCI] 백준 3055 - 탈출 (0) | 2021.10.26 |
|---|---|
| [KOI] 백준 2583 - 영역 구하기 (0) | 2021.10.25 |
| [ICPC] 백준 3860 - 할로윈 묘지 (0) | 2021.09.08 |
| [USACO] 백준 6002 - Job Hunt (0) | 2021.09.07 |
| [ICPC] 백준 4803 - 트리 (0) | 2021.08.24 |



