https://www.acmicpc.net/problem/2673
관찰
주어진 그림을 보자.
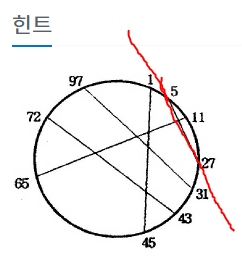
5~27을 무조건 연결한다고 가정하면 구간 [5, 27] 내의 점과 교차하는 현을 잇는 것은 불가능하다. 하지만 해당 구간을 벗어나는 현과는 연결할 수 있다.
다시 말해 어떤 현의 두 점이 구간 밖에 있으면 교차하지 않게 선택할 수 있다는 것이다. 아래의 그림처럼 어떤 현을 기준으로 했을 때 그 구간보다 작은 현들을 최대한 선택해야 함을 이해할 수 있다.
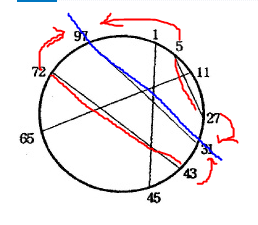
즉, 작은 구간에서 교차하지 않은 현의 최대 개수에서 큰 구간에서 교차하지 않는 현의 최대 개수로 누적하는 동적 계획법으로 생각할 수 있다.
헷갈리는 경우
만약 100과 1이 연결되어 있다고 해보자.
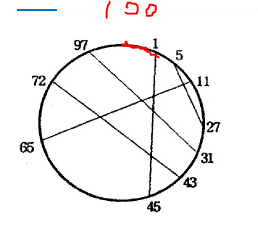
100~1의 길이는 작지만 구간으로 표현하면 [1, 100]으로 전체를 덮는다. 그래서 이런 현들에 의해 예외가 있지 않을까?라는 의문이 들 수 있다.
하지만 99~2, 98~3을 연결해보면 금방 알아차릴 수 있다.
[2, 99]는 [1, 100]보다 작은 구간, [3, 98]은 [2, 99]보다 작은 구간 이기 때문에 교차하지 않게 연결할 수 있게 된다.
따라서 우리는 100~1은 단순히 1~100으로 생각해서 풀어도 문제가 없음을 이해할 수 있다.
풀이
그러면 위의 관찰을 토대로 동적 계획법을 해보자. 점화식을 세우면 다음과 같다.
dp(i, j) := 구간 [i, j]에 속한 현들을 교차하지 않게 최대로 이은 갯수
이때 ischord(i, j)를 i와 j를 이은 현의 존재 여부라 하고 임의의 pivot k (i <= k <= j)를 잡으면 dp(i, j)는 다음과 같이 계산이 가능하다.
$dp(i, j) = max(dp(i, j), dp(i, k) + dp(k + 1, j) + ischord(i, j)) (i \leq k \leq j)$
교차하지 않아야 한다는 조건에도 불구하고 k에 i와 j를 포함하는 이유는 어차피 각 점에는 최대 한 개의 현만 연결되기 때문에 간편성을 위해 포함해도 되는 것이다. 만약 두 개 이상의 현이 연결된다면 위 식을 조금 바꿔야 할 것이다.
구체적인 식을 세웠으니 3차원 반복문으로 동적 계획법을 계산한 후 $dp(1, 100)$ 을 출력하면 된다.
전체 코드 - 변수명이 위 풀이에 쓴 것과 일치하지 않으니 유의하라 (j -> end)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,avx,avx2,fma")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("unroll-loops")
#include "bits/stdc++.h"
#include "ext/rope"
using namespace std;
using namespace __gnu_cxx;
using ll = long long;
using pii = pair<int, int>;
int n;
bool chord[101][101];
int dp[101][101];
void solve()
{
cin >> n;
for (int i = 0; i < n; i++)
{
int u, v;
cin >> u >> v;
chord[u][v] = chord[v][u] = true;
dp[u][v] = dp[v][u] = 1;
}
for (int i = 2; i <= 100; i++)
{
for (int j = 1; j <= 100 - i; j++)
{
int end = j + i;
for (int k = j; k < end; k++)
{
dp[j][end] = max(dp[j][end], chord[j][end] + dp[j][k] + dp[k + 1][end]);
}
}
}
cout << dp[1][100];
}
int main()
{
cin.tie(nullptr);
ios::sync_with_stdio(false);
solve();
}
|
cs |
제출 기록

보너스
COCI에 비슷한데 더 쉽게 풀리는 문제가 있다고 한다. 도전해보자.
https://www.acmicpc.net/problem/3102
3102번: 겹치지 않는 원
첫째 줄에 원의 개수 N이 주어진다. (1 ≤ N ≤ 1,000) 다음 N개의 줄에는 두 정수 Ci와 Ri가 주어진다. Ci는 i번째 원의 중심 좌표이고, Ri는 그 원의 반지름이다. (1 ≤ Ci, Ri ≤ 100) 두 원이 반지름과
www.acmicpc.net
'백준 > DP' 카테고리의 다른 글
| 백준 1657 - 두부장수 장홍준 (0) | 2022.05.30 |
|---|---|
| [KOI] 백준 10937 - 두부 모판 자르기 (0) | 2022.05.30 |
| 백준 1937 - 욕심쟁이 판다 (0) | 2021.11.08 |
| [ICPC] 백준 11066 - 파일 합치기 (0) | 2021.11.06 |
| [KOI] 백준 2616 - 소형기관차 (0) | 2021.11.05 |



