https://www.acmicpc.net/problem/32250
힌트 1
만약 먼저 앉은 사람이 아무도 없을 경우 아무 자리에나 앉을 수 있다.
이 조건이 대단히 중요하다.
힌트 2
최초로 사람을 배치한 이후, 규칙에 따라 사람을 배치하는데 나타나는 성질을 찾을 수 있는가?
풀이
먼저 사람을 아무 곳에 배치한다고 해보자.
그러면 그 사람을 기준으로 나눈 왼쪽 구간과 오른쪽 구간 $L$과 $R$을 얻을 수 있다.
$L$과 $R$에서 사람을 배치할 때는 문제의 규칙에 의해 다음과 같은 성질을 발견할 수 있다.
구간 $L, R$에서 첫 번째 사람이 놓인 기준점을 포함하여 각 사람과의 거리는 2 또는 3이다.
이는 거리를 가능한한 멀리 떨어트려야 한다는 조건을 만족시키기 위해 중앙에 배치하면서 다시 두 개의 구간으로 나뉘는 것이 반복되어 최종적으로는 거리가 2 또는 3을 유지하며 배치하기 때문이다. (1은 인접하게 되므로 불가하다.)
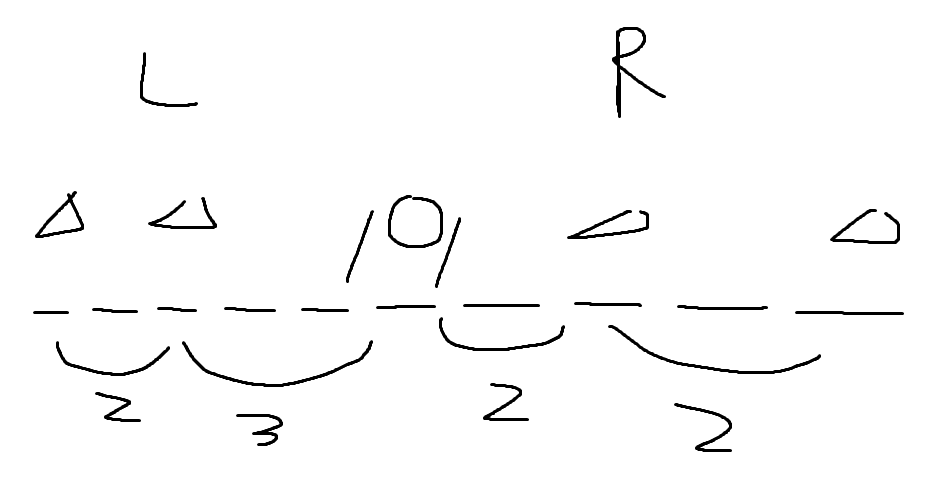
따라서 우리는 다음 함수를 정의할 수 있다.
$g(x) := $ 최초로 사람이 배치되서 나눠진 구간의 길이가 $x$일 때 규칙에 따라 배치할 수 있는 사람의 수
이 때 $g(x)$는 규칙에 따라 사람을 중간 지점에 배치 후 다시 둘로 나누는 과정을 통해 길이가 2 또는 3이 될 때까지 쪼개도록 할 수 있다.
$g(x)$를 구하는 과정에서 중복되는 계산이 발생하므로 동적 계획법을 사용하여 효율적으로 계산할 수 있다.
최초로 배치하는 위치에 따라 답이 달라질 수 있으므로 1부터 $N$까지 배치해보며 $MAX(1 + g(L) + g(R))$을 구하면 된다.
시간 복잡도: $O(N \log N)$
정답 코드 - pypy3
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
import sys
dp = dict()
def g(x: int):
if x <= 1:
return 0
if x <= 3:
return 1
if x in dp:
return dp[x]
l = x // 2
r = x - l
val = g(l) + g(r)
dp[x] = val
return dp[x]
def solve():
n = int(input())
ans = -10000009
for i in range(1, n + 1):
val = 1
l = i - 1
r = n - i
if l > 0:
val += g(l)
if r > 0:
val += g(r)
if ans < val:
ans = val
print(ans)
if __name__ == "__main__":
sys.setrecursionlimit(1000)
solve()
|
cs |
'백준 > DP' 카테고리의 다른 글
| 백준 12199 - Password Attacker (Large) (1) | 2024.11.19 |
|---|---|
| 백준 23280 - 엔토피아의 기억 강화 (1) | 2024.11.17 |
| 백준 1398 - 동전 문제 (1) | 2024.04.25 |
| 백준 2040 - 수 게임 (3) | 2022.09.28 |
| 백준 24457 - 카페인 중독 (0) | 2022.08.25 |

