728x90
아이디어
학창 시절에 배운 평면의 결정 조건을 기억하는가? 평면의 결정 조건 중에는 이런 것이 있다.
한 직선 위에 있지 않은 세 점
평면이 아닌 공간 위에서는 당연히 평면도형 또한 생겨날 수 없으므로 평행사변형이 만들어질 수 없는 경우를 결정할 수 있다.
1. 주어진 세 점이 한 직선 위에 있는 경우
2. 주어진 세 점의 좌표가 모두 동일할 경우
이 두가지의 경우 평면 도형을 만들 수 없으므로 -1을 출력해주는 조건이 된다.
그렇다면 나머지의 경우는 어떻게 될까? 한 점을 자유롭게 놓을 수 있으므로 무조건 평행사변형을 만들 수 있다.
그래서 어떻게 만드는데?
종이의 임의의 삼각형을 하나 그려보자.

그리고 점을 찍다 보면 다음과 같은 평행사변형들을 만들 수 있다.

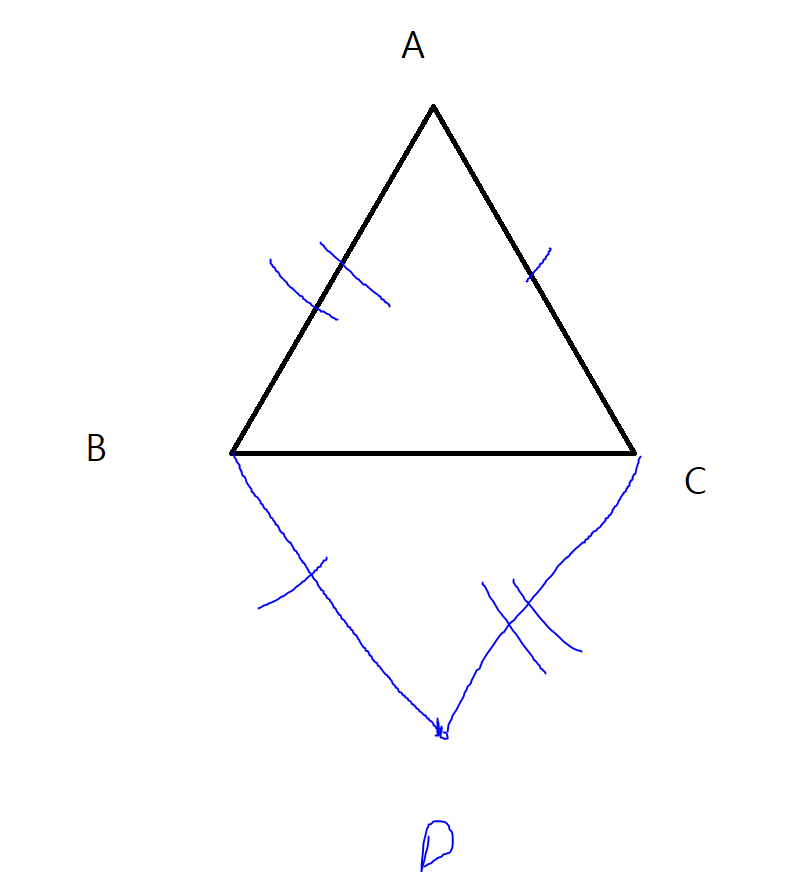

즉 평행사변형이 만들어지는 경우는 삼각형에서 두변을 선택해서 평행한 대변을 생성하는 경우이다.
평행사변형은 $\binom{3}{2} = 3$개가 생성되므로 3가지 평행사변형에 대해 둘레를 구해주고 최댓값 - 최솟값을 해주면 정답을 구할 수 있다.
전체 코드
본 소스에서 평면은 CCW를 사용하여 판별하였으나 단순 if문으로 같은 직선상에 있는지 검사해도 무방하다.
더보기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#include <iostream>
#include <algorithm>
#include <queue>
#include <utility>
#include <cmath>
using namespace std;
using pii = pair<int, int>;
int ccw(pii a, pii b, pii c)
{
return a.first * b.second + a.second * c.first + b.first * c.second - b.second * c.first - a.first * c.second - a.second * b.first;
}
int main()
{
cout.precision(16);
cout << fixed;
ios::sync_with_stdio(false); cin.tie(0);
vector<pii> parallelogram(3);
for (auto &item: parallelogram)
cin >> item.first >> item.second;
if (!ccw(parallelogram[0], parallelogram[1], parallelogram[2]))
{
cout << -1;
return 0;
}
vector<double> boundary;
for (int i = 0; i < 3; ++i)
{
for (int j = i + 1; j < 3; ++j)
{
double a = (parallelogram[i].first - parallelogram[j].first) * (parallelogram[i].first - parallelogram[j].first);
double b = (parallelogram[i].second - parallelogram[j].second) * (parallelogram[i].second - parallelogram[j].second);
boundary.push_back(sqrt(a + b));
}
}
sort(boundary.begin(), boundary.end());
cout << 2 * (boundary[2] - boundary[0]);
}
|
cs |

728x90
'백준 > 기하' 카테고리의 다른 글
| [ICPC] 백준 3861 - Slalom (0) | 2022.07.02 |
|---|---|
| [ICPC] 백준 9015 - 정사각형 (0) | 2022.06.08 |
| 백준 2022 - 사다리 (0) | 2022.04.03 |
| 백준 14400 - 편의점 2 (0) | 2020.06.26 |



